Analysis of Time-Resolved Crystallographic Data
Highlights from a 1996 thesis
Please cite this article as:
Krebs, W.G., "Kinetic Analysis and Intermediate Structure Determination
From High-Speed Time-Resolved Crystallography," MS Thesis, University
of Chicago, 1996.
and
Krebs, W.G., and Moffat, K., "Analysis of Time-Resolved Crystallographic
Data", HTML document, http://bioinfo.csb.yale.edu/~wkrebs/paper1/paper1.doc.
Werner G. Krebs* under supervision of Keith Moffat
Department of Biochemistry and Molecular Biology
The University of Chicago
920 E. 58th St. Chicago, IL 60637, USA.
Last Revision: May 1997.
*Present Address: San Diego Supercomputer Center Dept 0505, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0505, USA; email wgk@wernergkrebs.com.
Table of Contents
Abstract
Despite the very recent availability of Time-Resolved Crystallography
(TC) data sets, the promise of TC remains largely unfulfilled due to the
difficulty in extracting structural information on intermediates from time-resolved
electron density maps. These maps are only composites of the electron density
maps of the populated chemical species present at the experimental time
points. Although various schemes of extracting homogeneous structures from
TC data sets have been proposed, to date no structures have been determined.
In this paper we present novel methods for estimating these parameters
directly from a TC data set.
1. Introduction
Crystallographers have traditionally applied several techniques to obtain
detailed structural information on reaction intermediates. The most common
approach has been to design a series of stable structures that mimic normally
short-lived intermediates. However, these structures are stable precisely
because they are not identical to the intermediates they seek to mimic,
and key interactions are usually missing. Other experimental techniques
and chemical intuition are called upon to supply the missing information,
sometimes with only limited success.
Cryocystallography is a second, widely-used approach (Douzou and Petsko,
1984; Fink and Petsko, 1981; Makinen and Fink, 1977). Suitable adjustment
of temperature may alter the population and greatly prolong the lifetimes
of the intermediates, and thus allow their structures to be determined
by otherwise conventional crystallographic techniques. However, it may
be difficult to demonstrate that the trapped intermediates lie on the direct,
productive pathway at physiological temperatures.
Time-resolved Crystallography (TC), a complementary approach, uses an
intense synchrotron X-ray source to greatly reduce crystallographic exposure
times. The uses of synchrotron radiation in X-ray diffraction experiments
in macromolecular crystallography have been reviewed (Greenhough and Helliwell,1983;
Helliwell 1984; Helliwell, 1985). TC has the potential to offer detailed
structural information on short-lived intermediates in macromolecular reactions
under near-physiological, crystalline conditions, and this aids elucidation
of the underlying molecular mechanisms. Interpretation of TC data has been
hindered, in part due to the difficulty in extracting structural information
on intermediates from time-resolved electron density maps. Under certain
assumptions, these maps are weighted averages of the electron density maps
of the different structural species present at the experimental time points.
That is, these time-dependent electron density maps are structurally heterogeneous.
Moffat (1989) has proposed a strategy for extracting homogeneous structures
from time-resolved data sets, but this strategy has not yet been experimentally
tested.
Estimates are required of the time-dependent relative concentrations
and number of significantly populated, structurally distinct species (mathematical
components) represented in the TC data set, and a kinetic model for the
key intermediates must be developed. We previously relied on optical data
obtained on single crystals to generate the required model, with limited
success. Since the optical data need not exactly parallel the X-ray data
(Ng et al.,1995), it is clearly preferable to develop the kinetic model
and its associated parameters directly from the TC data. We present here
novel methods in reciprocal space that identify the number of structurally
distinct species present, the rate constants for their interconversion,
and possible kinetic models. In another paper, we apply these methods to
successfully extract structural information from a TC data set acquired
during decay from the saturated photostationary state of photoactive yellow
protein, PYP (Krebs 1996).
2. Principles of TC Data Analysis: Extraction
of Conformational Structure Information from TC Data in Reciprocal Space
In both conventional crystallography and TC, X-ray diffraction intensities
arise from a time average over all molecular conformations that exist during
an exposure time 
between 
and 
and from a volume average over all molecules illuminated. The volume average
is taken over all the molecules in the crystal and is effectively constant,
but in a TC experiment the conformations vary with time. Following Moffat
(1989), we assume that at time t after initiation of a structural
reaction the crystal contains a series of time-independent conformations
C1, C2, C3, ..., Ci, ..., with time-dependent fractional occupancies 
and structure factors 
for the reflection 
.
If the crystal exhibits random substitutional disorder, that is, conformations
Ci are distributed spatially at random in the real lattice, then the distribution
of Ci may be described as the convolution of the electron density of the
conformation Ci with a randomly sparse real lattice. The distribution of
conformations in the entire crystal is the sum over i of such convolutions,
and the total structure factor 
is then given by
1
for each reflection 
at time 
,
and 
for all values of 
.
Figure 1 illustrates Equation 11 diagrammatically
for one reflection.
Also,
2
where we represent structure factors as two-dimensional, real-valued
vectors 
,
is the structure factor amplitude of the reflection 
at time 
,
and 
is the structure factor amplitude of the reflection 
corresponding to the time-independent conformation Ci.
If the values of 
and 
are known for sufficiently many time points 
,
Equation 2 can be solved for the right-hand real-valued parameters 
and 
for all Ci,j by any suitable method for solution of non-linear equations.
The values of 
are derived directly from the observed intensities in the reduced TC data
sets. The values of 
can potentially be derived from a number of sources, including subsidiary
optical measurements taken concurrently with the TC data (Ng et al., 1995),
and by the analytical methods we present below. In practice, it appears
effective to use a variant of non-linear least-squares optimization with
suitable constraints applied on the values of 
and 
.
The values of 
thus determined are the desired time-independent structure factor amplitudes
of the conformations Ci, and may be combined with known phase data for
one of the conformations to yield the desired conformations Ci by standard
difference Fourier techniques. Such techniques neglect small differences
in phase between conformations. If the dot product parameters in Equation
2 are known, techniques described in Appendix 4 sometimes enable phase
relationships to be determined more precisely. Consequently, the time-independent
structures can be determined provided the 
s
can be accurately derived.
The time dependence of the relative concentrations 
s
of a first-order reaction scheme with 
components are determined by a system of 
rate constant parameters plus 
initial relative concentration parameters, of which 
are independent. Thus derivation of a kinetic model potentially requires
determination of 
parameters in order to calculate 
relative concentrations for the 
time-points in Equation 4. In practice, an over-determined system with
time-points is required to solve Equation 4, so that our method is at least
as efficient as direct measurement of the 
s
in terms of the number of parameters that need be estimated.
Most few-component systems have considerably fewer than 
rate constants because a number of potential reaction pathways between
the system components can be ruled out by an a priori knowledge
of the system chemistry. For example, in the case of PYP the native structure
is stable (Ng et al. 1995), and appears to consist of only one structurally
homogenous conformation, the ground state. On the basis of this stability,
two of the six potential reaction pathways can immediately be ruled out,
and the number of parameters needing estimation is reduced further.
Recall from Appendix 1 that under certain assumptions
global exponential fitting can be applied to crystallographic data (Moffat,
1989) as a first step in the analytic determination of the values of the
s.
This is done by substituting Equation 14 of Appendix
1 into Equation 2 and obtaining:
3
where the new parameters are the pre-exponential vectors 
and associated real-valued dot-products 
.
where the 
are real-valued constants invariant over time 
,
while the 
parameters are invariant over both reflections 
and time 
.
By taking advantage of the large number of observations 
in a typical crystallographic data set, it is possible to determine both
the 
and 
parameters in Equation 3. An iterative approach is used that performs successive
improvements to the estimated 
s.
Given the estimated 
s
from the previous iteration of the method, for any reflection 
Equations 2 and 3 form systems of equations over the time-points 
in the TC data set. By using an appropriate solution technique such as
constrained LS optimization or SVD, the values of the 
or
can be computed in Equations 2 or 3 respectively for each reflection 
,
provided the number of values to be solved for does not exceed the number
of available time-points 
.
Due to experimental errors in the data and in the initial values of
the 
s,
the fit obtained will not be perfect. The remaining errors can be aggregated
over all reflections in the data set and used as a figure-of-merit value
for the estimated 
s.
A standard multidimensional optimizer such as the Powell conjugate gradient
methods (Press et al., 1992), can use this information to find successive
improvements on the 
s.
The end result of this procedure is that optimum values for the exponential
constants 
and pre-exponential constants 
are determined. The use of this technique is illustrated in Figure
3.
An obvious candidate for such a figure-of-merit function is simply the
aggregate sum of the figures-of-merit obtained in the fitting of each reflection
.
Unfortunately, this choice has a statistical disadvantage that is seen
in regression analyses of a similar nature (Brunger, 1992): the individual
summation terms were already optimized during the reflection fitting, so
little new information is added by this choice of global figure-of-merit.
In addition, we encountered a more practical problem derived from the standard
errors in the sigmas associated with each of the observed structure factor
amplitudes from the LaueView (Ren and Moffat, 1995) output. These problems
are overcome by using techniques such as statistical cross-validation.
3. Computationally Useful Linear Approximations
Linear approximations of Equations 2 and 3 which are very useful computationally
are possible if we disregard the small phase differences between the structure
factors of the conformations:
4
and,
5
If, as before, the number of components 
and the values for the relative concentrations 
s
are known in advance for all times 
,
Equation 4 reduces to a linear least-squares estimation which can be solved
by a suitable linear matrix method, such as singular value decomposition
(SVD). A similar statement can be made for Equation 5, if the values of
the 
s
instead of the 
s
are known. These processes are considerably faster than the non-linear
LS iterative methods generally required for Equations 2 and 3. Experience
has shown (Krebs, unpublished observations) that the estimates produced
by solving the approximate Equations 4 and 5 provide excellent initial
parameter estimates for the non-linear optimizers needed to solve Equations
2 and 3 and are often useful on their own merits.
4. Determination of the Kinetic Model
At this stage the number 
of distinct components has been established and the values for 
and 
have been estimated. The next and potentially most difficult step is to
establish the kinetic model, and to extract the desired structure amplitudes
from the fitted parameters 
and 
.
A number of degrees of freedom remain in the general kinetic model after
the 
s
have been determined. Chemical knowledge can often be used to eliminate
a few of these parameters, but in general there will be additional parameters
to be determined. We would like to obtain at least rough estimates of these
parameters using a purely analytical approach.
One would like to be able to develop a figure-of-merit function to evaluate
suggested values for these parameters and optimize their estimates, in
a similar manner to that used above to extract the exponential coefficients.
It is not clear that this can easily be done using recripical space analysis.
The structure factor amplitudes of the desired intermediate conformations
are immediately related to the values of 
and kinetic model parameters by means of the following relations easily
derived from the linear approximations of Equations 4 and 5 as follows:
6
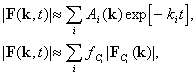
and therefore,
7
If the 
are estimated from the proposed kinetic model, this forms a system of 
equations with 
unknown values and can be solved for the values of 
by standard linear matrix methods. Specifically,
8
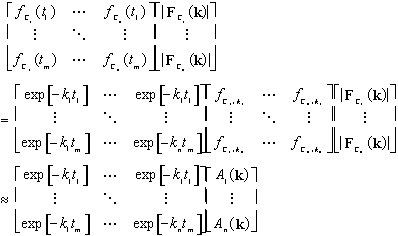
which implies
9
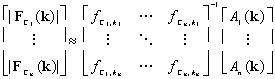
is one solution. Recall that the values of 
are determined or over-determined in a useful TC experiment via Equation
2, so this is normally the only solution.
Recall from Appendix 1 that in a first-order
system of 
components, the time-dependence of the relative concentration of any component
is a linear combination of 
or fewer exponential functions. The new parameters in Equation 7, the value
of 
,
represents the pre-exponential constant of the 
th
exponential term in the expression for the relative concentration of the
th
component. These constants form an 
matrix independent of reflection index 
which is derived solely from the kinetic model parameters. This matrix
is computed from the coefficients in the solution of the system of coupled,
linear ordinary differential equations that expresses the time-dependence
of each component in the proposed model to the is 
exponential functions and is invertible by construction.
The corresponding relation for the non-linear method is more complicated,
and is probably best handled computationally by fitting 
instead of 
to the data again, although no new information is derived. The results
of the linear approximation should be used as initial estimates for the
non-linear method in order to reduce the computational cost.
Application of Equation 7 allows rapid generation of structure factor
amplitudes from the already estimated 
values and the matrix of 
values that is defined by each proposed kinetic model. Thus, determination
of the remaining kinetic parameters by optimizer iteration over parameter
space could be computationally inexpensive were a suitable figure-of-merit
function available.
An immediately obvious candidate for the figure-of-merit function is
examination of the fitted structure factor amplitudes for plausibility.
Careful examination of Equation 7 suggests, and experience reveals (Krebs,
unpublished observations), that seriously incorrect 
values generate bogus 
values, and this affords one route for a plausibility check. A figure-of-merit
function based on the condition
10
is one possibility. In the analysis of test data discussed below, the
two potential figure-of-merit functions
11
and
12
were found to be potentially promising and allowed a subset of parameter
space to be ruled out. Of these two, the first proved more successful in
tests with simulated data.
A second approach involves real-space analysis and is potentially less
automated. Changes in the parameters which determine the kinetic model
result in changes in the values of 
,
which can be used to produce electron density maps by standard crystallographic
Fourier transform techniques. These maps can then be evaluated in real
space by structural inspection or by explicit crystallographic refinement
until satisfactory values for the remaining parameters in the model have
been found. That is, an authentic intermediate must itself be a single,
crystallographically refinable, macromolecular structure. This approach
evaluates in real space the kinetic model and its associated parameters
that were derived in reciprocal space.
5. Conclusions
Determination of relative concentrations of the desired intermediate
components at the time points 
in a TC data set is a difficult problem, but one that can be solved by
many methods. Experimental techniques such as time-resolved optical spectroscopy
have hitherto proved troublesome, hence the desire for means of determining
these values directly from the TC data.
The most promising approach, as in analysis of time-resolved spectroscopy
data, is determination of a kinetic model and related parameters for the
system under study. This is likely to be practical only for few-conformation
systems, but these are likely to be the only systems studied by TC at present.
Kinetic model determination as described herein consists of two steps,
each of which is based on a number of assumptions. The first step is determination
of exponential decay constants under the assumption that all conformations
interconvert obeying first-order or pseudo-first-order reaction laws.
Determination of the exponential decay constants proceeds by having
an optimizer iteratively suggest these values to a submodule, which then
attempts to fit pre-exponential coefficients to them. Aggregate errors
from the fittings are used to evaluate the merit of the parameters proposed
by the optimizer, which then uses these merit values to re-adjust its proposed
parameters as part of its iterative technique. This two-stage technique
allows global exponential fitting of TC data in 
time, where 
is the number of reflections fitted.
Additional parameters are required to fully determine the kinetic model.
These consist of the initial concentrations of the conformations, and additional
parameters, depending upon the model being analyzed. These parameters can
be filled in by a combination of a priori chemical knowledge, other
experimental techniques, and additional optimization analysis of the remaining
parameters.
Once the kinetic model has been identified, the number of conformations
in the system and the relative concentrations of these conformations for
all time points 
is known, the structure of macromolecule may be determined by applying
standard crystallographic techniques to the calculated structure factor
amplitudes of the desired intermediates. The entire process is depicted
diagrammatically in Figure 3.
Appendix 1: Mathematical Background
A general kinetic model for the interconversion of conformations has
the form,
13
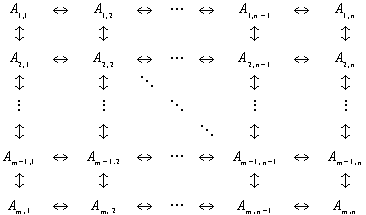
.The concentrations of the conformations obey the coupled ODE system,
14
where 
is the order of the kinetic pathway.
Reactions involving interconversion of conformations in large macromolecules
are likely to obey first-order kinetics, i.e. 
in Equation 14. Then we can prove several useful properties of the system.
Lemma 1
If the concentrations of all conformations A in the generalized first-order
reaction scheme Equation 13 except possibly some conformation B (where
B is one of the 
)
obey the time dependence
15
for finitely many 
,
then conformation B obeys this time dependence also.
Proof
By assumption, conformation B obeys the first-order reaction condition
16
where 
represents the rate constant by which some conformation 
decays into conformation B and 
represents the rate constants by which B decays into conformation 
.
Then, if we substitute Equation 16 into Equation 15, we obtain
17
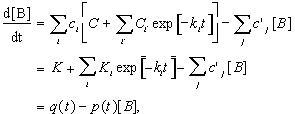
where 
and 
are new constants that replace 
and 
.
The last line in the equation was written to emphasize that the equation
can be written in standard form for a first-order linear differential equation,
and therefore all solutions are known to be of the form
18
where 
For simplicity of notation, let 
.
Then 
.
This gives:
19
The last line has the same form as Equation 15, with one additional
exponential.
(We have to assume 
to avoid a zero in the denominator of the integrand in Equation 19. This
pathological state, which would have resulted in a time dependence term
of the form 
,
can be avoided mathematically by ensuring that all rate constants differ
at least infinitesimally from any nonzero 
.
As 
,
the magnitudes of some terms of Equation 19 become very large and have
sums which nearly cancel out when added to give a term of the form 
in the limit. Since this is a rather unlikely situation physically, Equation
19 is usually an excellent approximation. It does illustrate a potential
problem, however, as very similar decay constants could result in arithmetic
overflows in algorithmic implementations of Equation 19. Since decay constants
capable of causing this problem are likely to be indistinguishable in the
experimental data, this does not represent a serious limitation to the
method, and in order to save space we will assume in the statement of Theorem
2 that 
differs infinitesimally from all 
in any real system.)
Theorem 2
If there are no cyclic pathways in Equation 13 (i.e., the scheme
forms a directed acyclic graph) then the time concentration of all conformations
obeys Equation 19.
Proof
Since there are no cyclic pathways and only finitely many conformations,
there must exist initial conformations A which have no precursors. Then
since we have assumed that all conformations obey simple first-order kinetics,
these conformations must simply decay from starting concentrations 
with time-dependence 
.
Now, assume there is some conformation whose concentration does not
obey the time-dependence given by Equation 19. Then, by the contrapositive
of the lemma, there exists at least one other conformation whose concentration
does not obey the time-dependence of Equation 19. Since there are no cyclic
pathways, and since there are only finitely many conformations, we can
continue by induction in this manner until we have shown that all conformations
do not obey Equation 19.
But, we just stated that there exist initial conformations A which obey
Equation 19. Therefore, all conformations must obey the time dependence
given by Equation 19.
The proof of the lemma also gives us the following important theorem:
Theorem 3
In an acyclic first-order reaction scheme, the number of summation
terms in Equation 19 is at most equal to the number of conformations in
our system.
Proof
In mathematical graph theory, it is shown that the nodes in a directed
acyclic graph can be visited in such a way that all of the ancestors, or
inputs, of any state can be visited before that state itself need be visited
(Cormen et al., 1990). Chemically, this means that, because our reaction
scheme is acyclic, we can first compute the explicit time-dependencies
of all precursors of a conformation without first knowing the time-dependency
of the state itself.
We have shown that there are first-generation initial conformations
A whose concentration varies as a single exponential. Graph theory tells
us that we can find the time-dependencies of the concentrations of these
second-generation conformations, whose only precursors are first-generation
initial conformations. Inspection of the proof of the lemma reveals that
these second-generation conformations can vary at most as the sum of two
terms of Equation 19, and that each additional generation can vary at most
as the sum of one term more than the previous generation. Since the number
of generations in our scheme can be no greater than the number of conformations,
the number of summation terms in Equation 19 is at most equal to the number
of conformations in our system.
These statements are actually more general than this, and hold for some
chemical systems with cycles, a fact which will not be proved here.
Return briefly to our original assumption of first-order kinetics. The
useful properties of first-order reaction schemes just proved are due in
large part to properties of the integrand of the exponential function.
Systems which are not first-order will almost certainly not have these
properties.
As an illustration, consider the simple decay of an initial conformation
via a single, non-first-order path. For simplicity, we will again assume
the simple kinetics of Equation 14 which in the case of an initial conformation
degenerates to:
20
Solving this differential equation yields:
21
where 
is the order of the reaction and 
is some constant algebraically related to the initial concentration of
the conformation. Thus, even for these relatively simple systems, precise
expressions of the time-dependence of their concentrations will quickly
become impossible as system complexity increases, and more radical approximations
must be used for these systems than was necessary in our analysis of first-order
systems here. Similar conclusions can be arrived at by consideration of
virtually any other commonly used non-first-order kinetic model. Consequently,
it is essential that the majority of reactions dealt with in TC data obey
at least approximately first-order kinetics if our technique is to be useful.
Appendix 2: Extraction of Some Structures Without
Complete Kinetic Information
Under some circumstances it is possible to obtain structures of only
a portion of the conformations present. Consider the following reaction
scheme:
22
In this scheme, conformation A has no logical ancestor in the graph
of the reaction scheme. It can be thought of as a ìrootî conformation,
and its concentration obeys the simple exponential decay law:
23
where 
is the sum of the time constants of all decay pathways of A. We know from
the theorem in Appendix 1 that 
is one of the 
exponential constants determinable by our method of TC global exponential
fitting. If we now think of A as part of a two-state chemical system:
24
where A is a root conformation and B describes the chemical state when
the molecule is not in the A conformation, not necessarily a homogenous
conformation. Then 
.
From Equation 4,
25
and we can solve this system for 
(We also determine 
in the process, but this is not necessarily a homogeneous conformation
and is thus less useful.). We refer to this process as the "peel-away"
method, since successive conformations can be ìpeeled awayî
with this method.
In principle, it would have also been possible to determine 
by setting up the 
conformation system in Equation 4. However, doing has several disadvantages.
Simultaneously extracting all components requires accurate values of 
for all conformations present. This is normally only possible if the reaction
scheme is well understood, and extracting structures of only one or two
conformations using the two conformation system in Equation 24 is consequently
more robust against errors in the relative concentrations. In addition,
this "peel-away" method can be applied to obtain information
on initial conformations even in the absence of a kinetic model. Each exponential
rate constant can be tested to see if it represents an initial conformation
with no significant back-pathways by attempting to "peel-off"
the conformation and examining the resulting electron density map to see
if it appears to represent homogenous protein density. Usually any reasonable
initial concentration will do, thanks to the robustness of the method.
A second advantage of using a two-conformation system is that greater
completeness of data can be achieved with this method. We required that
Equation 4 be overdetermined when solving for the values of 
.
For a three-conformation system, this means that each reflection 
must have data available for at least four time points in addition to phase
information whereas when solving the two-conformation system, we only require
information to be available at three time points in addition to phase information.
Once the root conformations have been determined, the "peel-away"
method can then be applied recursively to the conformations further along
in the graph of the reaction scheme by transforming the 
s
appropriately to simulate two-component systems. In this way, any reaction
scheme without back-pathways can be solved using the "peel-away"
method, with all the advantages this entails.
One potential disadvantage of the "peel-away" method is that
errors may accumulate as further and further conformations are "peeled-off"
the TC data. This is easily corrected by refining previous conformations
and then using calculated (and, presumably, error-free) structure factor
amplitudes from these earlier stages to "peel-away" further conformations.
In this way, errors can be kept approximately constant throughout the process.
Appendix 3. Relationship of Crystallographic
Time-resolved Methods to Optical Spectroscopy Time-resolved Methods
Equation 5 looks so similar to the standard form for the exponential
decays found in quantitative analysis of optical data that it may seem
tempting at first to apply standard analysis techniques from time-resolved
optical spectroscopy rather than the techniques we present here. One practice
in time-resolved optical spectroscopy would express Equation 5 in matrix
form (Hoff, 1994):
26
where 
is an 
matrix measured across 
time points and 
reflections, 
denotes a matrix of error terms, and 
is the singular value decomposition of the matrix 
.
Then the exponential functions 
will generate the basis vectors for the matrix 
which will consist merely of that particular exponential sum evaluated
at all 
time points. The number of exponentials is nominally equally to the number
of conformations 
present in the system, so 
.
With perfect data 
,
and 
.
In practice 
is estimated by examining the matrix 
,
which is a diagonal 
matrix whose diagonal values give the relative amplitudes of the basis
vectors encoded in matrices 
and 
.
Some arbitrary constant is chosen (10-6 is common and comes from the expected
round-off error in double precision division; 10-3 might be more reasonable
for real data) and diagonal elements whose magnitude is less than this
constant times the magnitude of the largest diagonal are considered equivalent
to zero and discarded as noise. The number of remaining diagonal elements
constitutes 
.
We could in principle determine the number of conformations in the TC
data by simply taking an SVD of the matrix 
.
This method has been applied with great success to time-resolved optical
data (Hoff, 1994), but this method presents a number of serious difficulties
when applied to TC data.
One problem is that TC data reduction algorithms generate widely distributed
error estimates for individual reflections 
due to the wide range of errors in a typical TC dataset. There is no obvious
way of incorporating error estimates into this method of rank determination
by SVD. Consequently, very noisy data will be treated identically to high
quality data, and this creates the potential of identifying spurious components
by the method. This is not an issue in time-resolved spectroscopy, where
error levels are comparable throughout the dataset. However, the method
may be used in some TC applications to place a crude upper bound on 
.
A second problem is that the size of the matrix 
is several orders of magnitude larger than typical for time-resolved spectroscopy.
This can present data storage problems, as SVD can have 
memory requirements. A more serious problem is that SVD, essentially a
matrix inversion algorithm, is an 
method in terms of computational time. Experiment has shown that with typical
TC data (Krebs, unpublished observations) this method requires orders of
magnitude more computational time than a direct extraction of exponential
decays by the global exponential fitting method outlined above, which is
with the number of reflections.
A second method applied in optical spectroscopy (Knutson, 1983). involves
the equivalent of simultaneous determination of both the exponential decay
coefficients 
and also the pre-exponential amplitudes 
in Equation 3 in a single invocation of a non-linear least-squares optimizer.
The resulting figure-of-merit function is then a simple sum of quadratic
terms for each optimized parameter information. Partial derivatives of
the figure-of-merit function with respect to all parameters are easily
computable, and these could be used to accelerate optimization, at least
in principle. This approach allows all parameters to be determined with
a single invocation of an efficient least-squares optimizer, and is readily
applicable in optical spectroscopy where the total number of parameters
estimated is usually small. Again, typical TC data sets are unfortunately
much larger, and might have observations for more than 8000 reflections
over seven time points, so that the optimizer would be expected to estimate
over 
or 
parameters. The types of Levenburg-Marquardt optimizers used for typical
non-linear least-squares would store estimated second derivatives in a
Hessian of 
values and attempt to invert this matrix; this is again an 
process with 
memory requirements. This type of optimization is inefficient with TC data
because it implicitly assumes that the errors in all parameters are potentially
related, so that no parameter can be considered well-estimated until all
parameters are well-estimated. In fact, estimates of the 
s
for any reflection are affected only by errors in estimates for the exponential
decays, not by errors in the 
s
for fits on any other reflections. Again, global exponential fitting takes
advantage of this and is 
with the number of reflections, whereas the method described in this section
would be very inefficient if applied to TC data.
We assumed above that the number of conformations 
in our TC data was known in advance, and indeed, the crystallographer frequently
has some notion of a reasonable maximum number of conformations based on
a priori knowledge of the system chemistry. Our method can be first
applied with the estimated number of components 
set slightly larger than the anticipated number of components. The significance
of each of the 
values of 
estimated by the process is tested by examination of the RMS values of
the pre-exponentials 
and the magnitude of the 
s
themselves. Insignificant 
s
are eliminated and the method is re-applied with a reduced value of 
with the estimated values of the significant 
s
as new starting values. This process is repeated until both 
and the 
s
have been estimated to the satisfaction of the experimenter.
Appendix 4: Extraction of Partial Time-Resolved
Phase Information from TC data
The dot product parameters in Equation 2, if known, enable us to determine
the phase relationships more precisely (Moffat 1989). Now 
,
where 
is the difference in phase angles between the structure factors corresponding
to Ci and Cj. If we define 
,
then
27
Thus, the absolute values of the relative phase differences between
the structure factors can be determined, at least in principle, for all
values of 
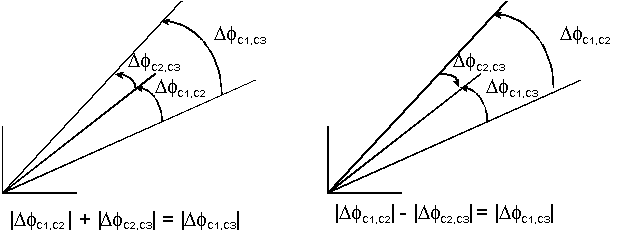
With three or more components, some information on signs can even be extracted
by noting that 
.
Then, if 
we must have 
,
and 
by the triangle inequality. Therefore, if we obtain numerically that 
or 
we know that 
and vice-versa; only some combinations of signs and relative phase differences
are possible. This is illustrated in Figure 2. Ideally,
this partial information on phase angle differences would be fed into a
real-space refinement process, to further enhance refinement and to assist
in determination of the correct phases of the structure factors corresponding
to each of the conformations. At the very least, Equation 27 could be used
to place suitable constraints on the values of the 
dot products obtained numerically as parameters during optimization of
Equation 2.
Figures
Figure 1: Diagram of structure factors varying
over time. On the left are a series of structure factor corresponding to
four different time points, labeled C1, C2, C3, C4. The diagram on the
right illustrates how these structure factors might evolve over time. After
Moffat 1989.
Figure 2: Diagram depicting how partial information
on phase angle signs can be extracted. On the left is illustrated the fact
that when two phase angles have the same sign, a third phase angle must
also have the same sign and must have magnitude equal to the sum of the
magnitudes of the first phase angles. The diagram on the right indicates
what happens when the phase angles have different signs; in this case,
a third phase angle has magnitude equal to the difference of the magnitudes
of these phase angles. Comparision of the magnitudes of these three phase
angles thus reveals partial information on their corresponding signs, as
described in the text.
Figure 3: Schematic diagram of conformation extraction
process. Shown here are the major steps involved in extraction of conformations
from TC data. The "Peel-Away" method is a modification of the
methods in this article and is described in Appendix
2.
References
- Brunger, A. T. 1992. Nature. 355:472.
- Cormen, T. H., Leiserson, C. E., Rivest, R. L. 1990. Introduction
to algorithms. Cambridge, Mass: MIT Press.
- Douzou, P., Petsko, G. A. 1984. Adv. Protein Chem. 36:246.
- Fink, A. L., Petsko, G. A. 1981. Adv. Enzymol. 52:177.
- Genick, U. K. Genick, Borgstahl, G. E. O., Ng, K., Ren, Z., Pradervand,
C., Burke, P. M., Srajer, V., Teng, T.-y., Schildkamp, W., McRee, D. E.,
Moffat, K., Getzoff, E. D. 1997. Science. 275:1471
- Greenhough, T., Helliwell, J. R. 1983. Prog. Biophys. Mol. Biol.
41:67.
- Helliwell, J. R. 1984. Rep. Prog. Phys. 47:1403.
- Helliwell, J. R. 1985. J. Mol. Struct. 130:63.
- Hoff, W. D., van Stokkum, I. H. M., van Ramesdonk, H. J., van Brederode,
M. E., Brouwer, A. M., Fitch, J. C., Meyer, T. E., van Grondell, R., Hellingwerf,
K. J. 1994. Biophys. J. 57: 1691.
- Krebs, W. G. Unpublished observations.
- Knutson, J. R., Beecham, J. M., Brand L. 1983. Chem . Phys. Lett.
102:501.
- Krebs, W. G. 1996. Masterís Thesis, Chicago: University of Chicago.
- Makinen, M. W., Fink, A. L. 1977. Anu. Rev. Biophys. Bioeng.
3:1.
- Moffat, K. 1989. Annu. Rev. Biophys. Biophys. Chem. 18:309.
- Ng, K., Getzoff, E. D., and Moffat, K. 1995. Biochemistry. 34:879.
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., Flannery, B. P.
1992. Numerical Recipes in FORTRAN. Cambridge, England: Cambridge
University Press.
- Ren, Z., Moffat, K. 1995. J. Appl. Crystalo. 28:461.
- Ren, Z. Unpublished observations.
Acknowledgements
I would like to thank Dr. Keith Moffat for the opportunity to work on
this project; Dr. Keith Moffat, Dr. Marvin Makinen, and Dr. Dean Astumian
for helpful comments on this manuscript; Dr. Keith Moffat, Dr. Zhong Ren,
Dr. Vukica Srajer, Ben Perman, Dr. Xiaojin Yang, Dr. Feng Zhou, Dr. Kingman
Ng, and Dr. Tsu-Yi Teng for many helpful discussions; Dr. Keith Moffat,
Dr. Feng Zhou and Ben Perman for providing datasets used in the analyses.
Questions or comments about this web page should be sent to werner.krebs@yale.edu.
Copyright (C) 1997 Werner G. Krebs. All Rights Reserved.